
Оценивание неопределенности измерений (количественных величин) – одна из важных задач, стоящих перед каждой лабораторией. Требование к оцениванию неопределенности измерений заложено в межгосударственном стандарте ГОСТ ISO/IEC 17025-2019, а также политике ILAC-G17:2002.
Чтобы получить предварительную информацию по теме Неопределенность измерений, посмотрите, пожалуйста, наше обучающее видео:
Международное метрологическое сообщество давно уже разработало и приняло основные принципы концепции неопределенности, закрепив их в серии международных документов JCGM (Joint Committee for Guides in Metrology), а также документах ISO/IEC Guide 98. Разработано много дополнительных руководств по различных подходам оценивания неопределенности измерений в конкретных областях испытаний/измерений (EA, EURACHEM, Nordtest, EUROLAB и т.д.).
Несмотря на хорошо разработанные и представленные в документах свободного доступа теоретические принципы и подходы оценивания, и даже наличия конкретных примеров, у специалистов лабораторий все еще остаются вопросы по практической реализации этих принципов и подходов для измерений, проводимых в их лаборатории.
С целью наглядного представления основных принципов концепции неопределенности измерений и подхода моделирования предлагаем Вашему вниманию решение нескольких несложных, но часто встречающейся в практике многих испытательных лабораторий, задач:
Пример 1. Оценивание неопределенности измерений массовой доли влаги
Исходные данные:
- Объект измерений – углекислый барий
- Измеряемая величина – массовая доля влаги
- Единицы измерений – процент (%)
- Методика выполнения измерения – ГОСТ 2149-75 «Барий углекислый технический. Технические условия»
- Метод измерений – метод высушивания пробы до постоянной массы
Этап 1. Составление функции измерений
Функция измерений для измеряемой величины составляется на основании принципа измерений, заложенного в методе измерений, и описанного для реализации в методике выполнения измерений.
Массовую долю влаги бария углекислого Х в процентах вычисляют на основании ГОСТ 2149 (п.3.5) в соответствии с функцией измерений:


где Хi – массовая доля влаги i-ой пробы углекислого бария, %;
m1 – масса стаканчика для взвешивания с навеской до высушивания, г;
m2 – масса стаканчика для взвешивания с навеской после высушивания, г;
m – масса навески углекислого бария, г;
mcт – масса стаканчика для взвешивания, г;
i – номер параллельной пробы, i = 1, 2;
F – поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями.
Этап 2. Анализ входных величин
1) Масса стаканчика для взвешивания с навеской до высушивания, m1
Масса стаканчика для взвешивания с навеской до высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы m1(1) = 41,0055 г,
- для второй пробы m1(2) = 41,3842 г.
Неопределенность, связанную с величиной m1, оцениваем, используя данные производителя на весы. В паспорте на весы лабораторные AV264C для диапазона измерений до 50 г указаны пределы погрешности взвешивания ± 0,001 г. Поскольку значение дано без доверительной вероятности, принимаем прямоугольное распределение значений погрешности взвешивания в этих границах. Стандартная неопределенность массы стаканчика для взвешивания с навеской до высушивания m1 оценивается по типу В и составляет:

2) Масса стаканчика для взвешивания, mcт
Масса стаканчика для взвешивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы mст(1) = 21,0034 г,
- для второй пробы mст(2) = 21,3822 г.
Неопределенность массы стаканчика для взвешивания после высушивания обусловлена двумя факторами:
погрешностью взвешивания стаканчика на весах;
возможными отклонениями массы стаканчика после высушивания вследствие нечеткого определения в методике выполнения измерений момента, в который масса стаканчика после высушивания будет являться постоянной величиной.
Стандартная неопределенность u1(mcт), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m1 и составляет u1(mcт) = 0,00058 г.
Стандартную неопределенность u2(mcт), обусловленную отклонениями массы стаканчика для взвешивания после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса стаканчика после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(mcт) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:

Суммарную стандартную неопределенность величины mcт находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:

3) Масса стаканчика для взвешивания с навеской после высушивания, m2
Масса стаканчика для взвешивания с навеской после высушивания определяется путем взвешивания на весах лабораторных AV264C. При измерении влажности двух проб бария углекислого были получены следующие значения входной величины:
- для первой пробы m2(1) = 40,9850 г,
- для второй пробы m2(2) = 41,3638 г.
Неопределенность массы стаканчика для взвешивания с навеской после высушивания обусловлена двумя факторами:
- погрешностью взвешивания пробы на весах;
- возможными отклонениями массы пробы после высушивания вследствие нечеткого определения в методе испытаний момента, в который масса пробы после высушивания будет являться постоянной величиной.
Стандартная неопределенность u1(m2), связанная с погрешностью взвешивания, оценивается на основании данных производителя на весы лабораторные AV264C, определяется аналогично неопределенности величины m2 и составляет u1(m2) = 0,00058 г.
Стандартную неопределенность u2(m2), обусловленную отклонениями массы стаканчика для взвешивания с навеской после высушивания, можно определить на основании информации о том, что разность между двумя последующими взвешиваниями стаканчика для взвешивания с навеской пробы бария углекислого после сушки не должна превышать 0,002 г (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает момент, в который масса пробы после высушивания будет являться постоянной величиной). Это значение можно рассматривать как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения (предел повторяемости по СТБ ИСО 5725-6). Стандартная неопределенность u2(m2) будет равна стандартному отклонению, рассчитанному на основании указанного интервала по типу В по формуле:

Суммарную стандартную неопределенность величины m2 находим путем суммирования квадратов стандартных неопределенностей перечисленных выше двух вкладов:

4) Поправочный множитель, учитывающий допускаемое расхождение между параллельными определениями, F
Значение оценки величины принимается равным единице: F = 1.
Стандартная неопределенность поправочного множителя рассчитывается на основании информации о допускаемом расхождении между параллельными определениями влажности, приведенными в ГОСТ 2149-75 (п.3.5.2). Приведенное допускаемое относительное расхождение составляет r = 20 % и рассматривается как 95-% доверительный интервал для разности двух оценок величины, распределенной по нормальному закону распределения. Стандартная неопределенность поправочного множителя будет равна стандартному отклонению, рассчитанному на основании указанного интервала, с учетом того, что за результат измерения принимают среднее арифметические определений двух параллельных проб, по типу В по формуле:

Этап 3. Анализ корреляций
Все входные величины рассматриваются как некоррелированные, поскольку получены независимо друг от друга в различных экспериментах.
Этап 4. Измеренное значение величины
Массовая доля влаги i-ой пробы углекислого бария рассчитывается по формуле (2):
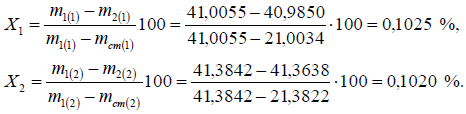
Расхождение между результатами измерений двух параллельных проб не превышает допускаемого значения, установленного в ГОСТ 2149-75 (п.3.5.2):
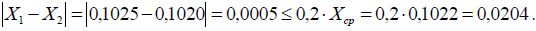
Массовая доля влаги бария углекислого Х в процентах вычисляется в соответствии с функцией измерений (1):
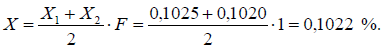
Измеренное значение (оценку измеряемой величины) округляют до четырех знаков после запятой (принято лабораторией, поскольку ГОСТ 2149-75 четко не устанавливает требования к округлению результата измерения).
Этап 5. Суммарная стандартная неопределенность
Стандартную неопределенность измеряемой величины Х получаем по закону распространения неопределенностей путем суммирования квадратов произведений стандартных неопределенностей всех влияющих величин, входящих в функции измерений (1) и (2), на соответствующие коэффициенты чувствительности:
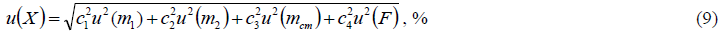
где коэффициенты чувствительности рассчитываются как частные производные функции измерений по входным величинам:
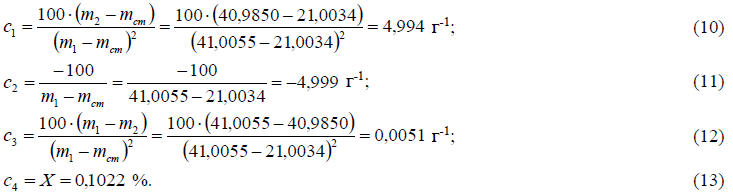
Примечание – Для вычисления коэффициентов чувствительности можно использовать либо минимальные значения масс, полученные при измерении массовой доли влаги i-ой пробы бария углекислого, либо результаты измерений масс, полученные на определенной пробе бария углекислого. В данном примере коэффициенты чувствительности рассчитываются на основании результатов измерений масс для первой пробы.
Суммарная стандартная неопределенность составит
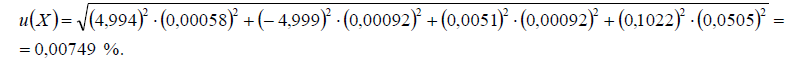
Этап 6. Бюджет неопределенности
В таблице представлен бюджет неопределенности для измеряемой величины.
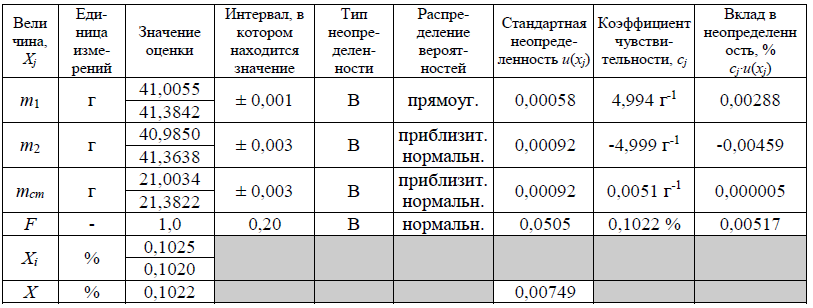
Вклад в неопределенность от j-ой входной величины рассчитывается как произведение стандартной неопределенности этой величины на соответствующий коэффициент чувствительности.
Этап 7. Расширенная неопределенность
Расширенную неопределенность U получаем умножением суммарной стандартной неопределенности на коэффициент охвата k, который выбирается равным 2 при уровне доверия приблизительно 95 % в предположении нормального распределения вероятностей измеряемой величины:

Этап 8. Представление результата измерения
Результат измерения массовой доли влаги углекислого бария представляют в виде:
«Массовая доля влаги бария углекислого составила (0,1022 ± 0,0150) %, где число, следующее за знаком ±, является численным значением расширенной неопределенности, которая получена умножением суммарной стандартной неопределенности на коэффициент охвата k = 2, основанный на предполагаемом нормальном распределении, и определяет интервал, соответствующий вероятности охвата приблизительно 95 %».

